Summary of Data Structures
Summary of Data Structures
Nama : Brian Eniko Singgih
NIM : 2301875074
Kelas : CB01
Lecturer : Ferdinand Ariandy Luwinda (D4522) dan Henry Chong (D4460)
Linked List
1. Circular Single Linked List
Circular single linked list adalah single linked list yang tidak menerima value NULL yang dikarenakan node terakhir akan menunjuk ke head pointer sehingga circular single linked list tidak menerima value NULL.

2. Doubly Linked List
Doubly linked list adalah single linked list yang memiliki 2 arah pointer dimana sebuah node memiliki 2 pointer yaitu next dan prev.

Ada 2 cara untuk menyunting doubly linked list:
a. Insert
Insert digunakan untuk memasukan node baru ke dalam doubly linked list dan mengkoneksikan node tersebut dengan node yang sudah ada.
struct tnode *node = (struct tnode*) malloc (sizeof (struct tnode);
node->value = x;
node->next = NULL;
node->prev = tail;
tail->next = node;
tail = node;
b. Delete
Delete digunakan untuk menghapus node tertentu dari doubly linked list.
Jika menghapus node saja:
free (head);
head = NULL;
tail = NULL;
Jika menghapus head:
head = head.next;
free (head.prev);
head.prev = NULL:
Jika menghapus tail:
tail = tail.prev;
free (tail.next);
tail.next = NULL;
3. Circular Doubly Linked List
Circular Doubly Linked List adalah gabungan dari circular single linked list dan doubly linked list. Di dalam circular doubly linked list sebuah node mempunyai 2 arah pointer dan tidak menerima value NULL atau node terakhir menunjuk ke head pointer.

Stack and Queue
Konsep Stack dalam data struktur:
1. Push()
Push berfungsi untuk memasukkan data.
Ada beberapa push dalam data struktur:
A. PushHead()
Push Head berfungsi untuk memasukkan data dari head. Contoh:
Ada terdapat linked list dengan node berikut:
10, 20.
10 adalah head dan 20 ada tail dan curr.
Jika saya ingin melakukan push head dengan value 30, maka linked list diatas akan menjadi:
30, 10 , 20.
30 adalah head dan 20 tetap tail dan curr,
B. Push Tail()
Push Tail befungsi untuk memasukkan data dari tail. Contoh:
Ada terdapat linked list dengan node berikut:
10, 20.
10 adalah head dan 20 ada tail dan curr.
Jika saya ingin melakukan push tail dengan value 30, maka linked list diatas akan menjadi:
10 , 20, 30.
10 tetap menjadi head dan 30 menjadi tail dan curr,
2. Pop()
Pop berfungsi untuk menghapus data.
Ada beberapa pop dalam data struktur:
A. Pop Head
Pop Head berfungsi untuk menghapus head di sebuah linked list.
B. Pop Tail
Pop Tail berfungsi untuk menghapus tail di sebuah linked list.
Hashing, Hash and Binary Tree
Hashing
Hashing adalah teknik yang digunakan untuk secara unik mengidentifikasi objek tertentu dari sekelompok objek serupa. Hashing dilakukan dengan membuat fungsi hash. Hasil dari fungsi hash dimasukkan ke dalam hash table.
Hash Table adalah salah satu contoh implementasi linked list dalam data struktur. Hash table digunakan dalam penyimpanan data sementara.
Ada banyak cara untuk hashing string ke sebuah key:
1. Mid-square
2. Division (most common)
3. Folding
4. Digit Extraction
5. Rotating Hash
Contoh hash table yang kurang efisien dan yang efisien:
Contoh yang kurang efisien

Contoh fungsi hash yang efisien:
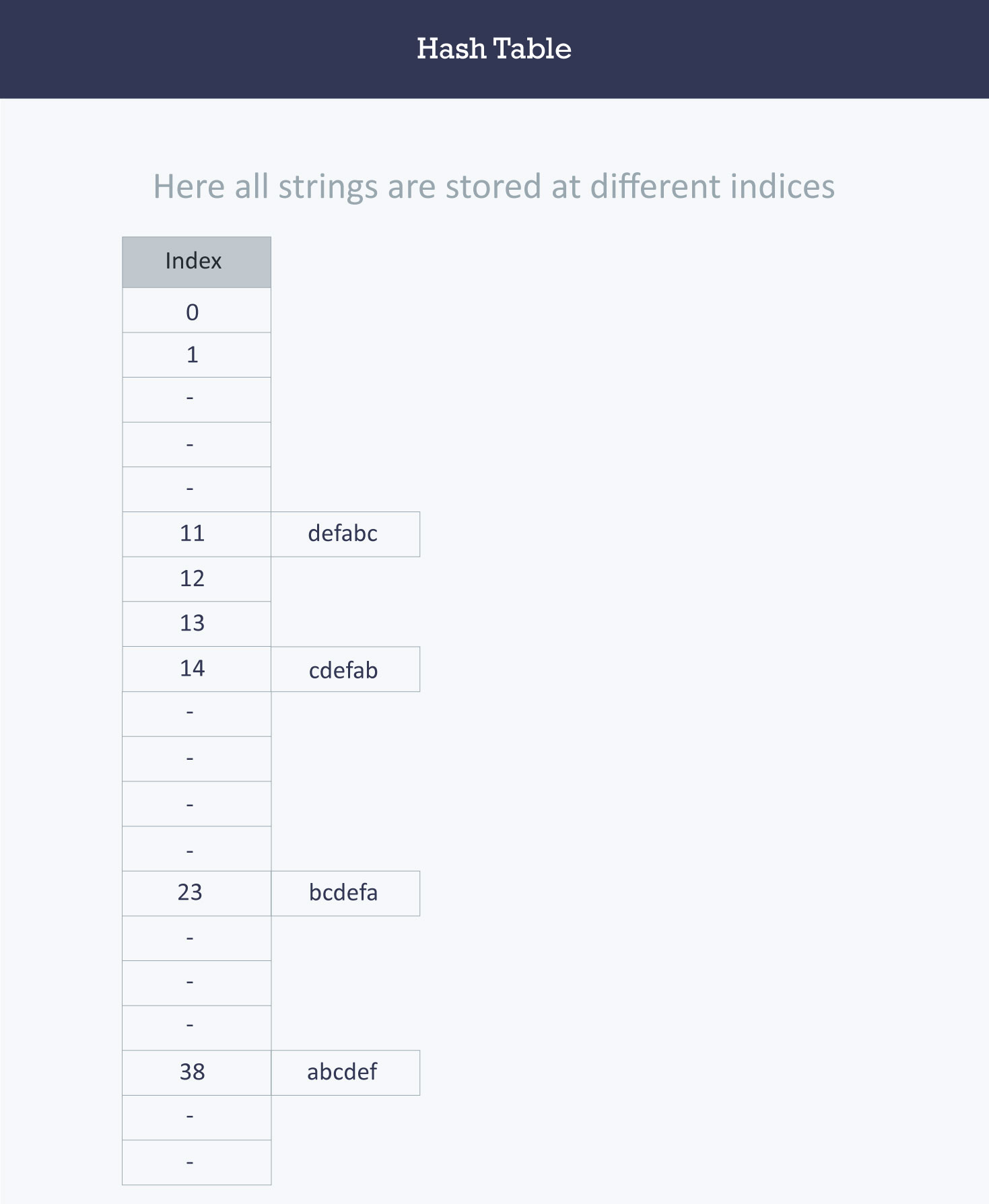
Sebaik apapun fungsi hash yang kita buat, collision tidak dapat dihindari, oleh karena itu ada banyak teknik untuk menghindari collision:
1. Separate Chaining (Open Hashing)
Separate Chahining adalah teknik yang paling banyak digunakan untuk resolusi tabrakan. Separate Chaining biasanya diimplementasikan menggunakan linked list. Dalam Separare Chaining, setiap elemen dari hash table adalah linked list. Untuk menyimpan elemen ke dalam table hash, kita harus memasukkannya ke linked list tertentu. Jika ada collision (Dua elemen berbeda yang memiliki hash yang sama) maka kita harus menyimpan kedua elemen tersebut ke dalam linked list yang sama.
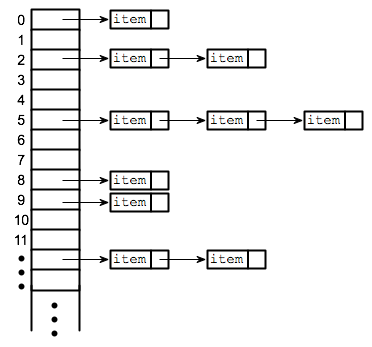

2. Linear Probing (Open Addressing or Closed Hashing)
Dalam Open Addressing, daripada menggunakan linked list, semua catatan entri disimpan dalam array itu sendiri. Ketika entri baru harus dimasukkan, indeks hash dari nilai hash dihitung dan kemudian array diperiksa (dimulai dengan indeks hash). Jika slot di indeks hash tidak diisi, maka entri dimasukkan ke dalam slot di indeks yang telah di hashed yang lain itu melanjutkan dalam beberapa urutan penyelidikan sampai menemukan slot kosong.
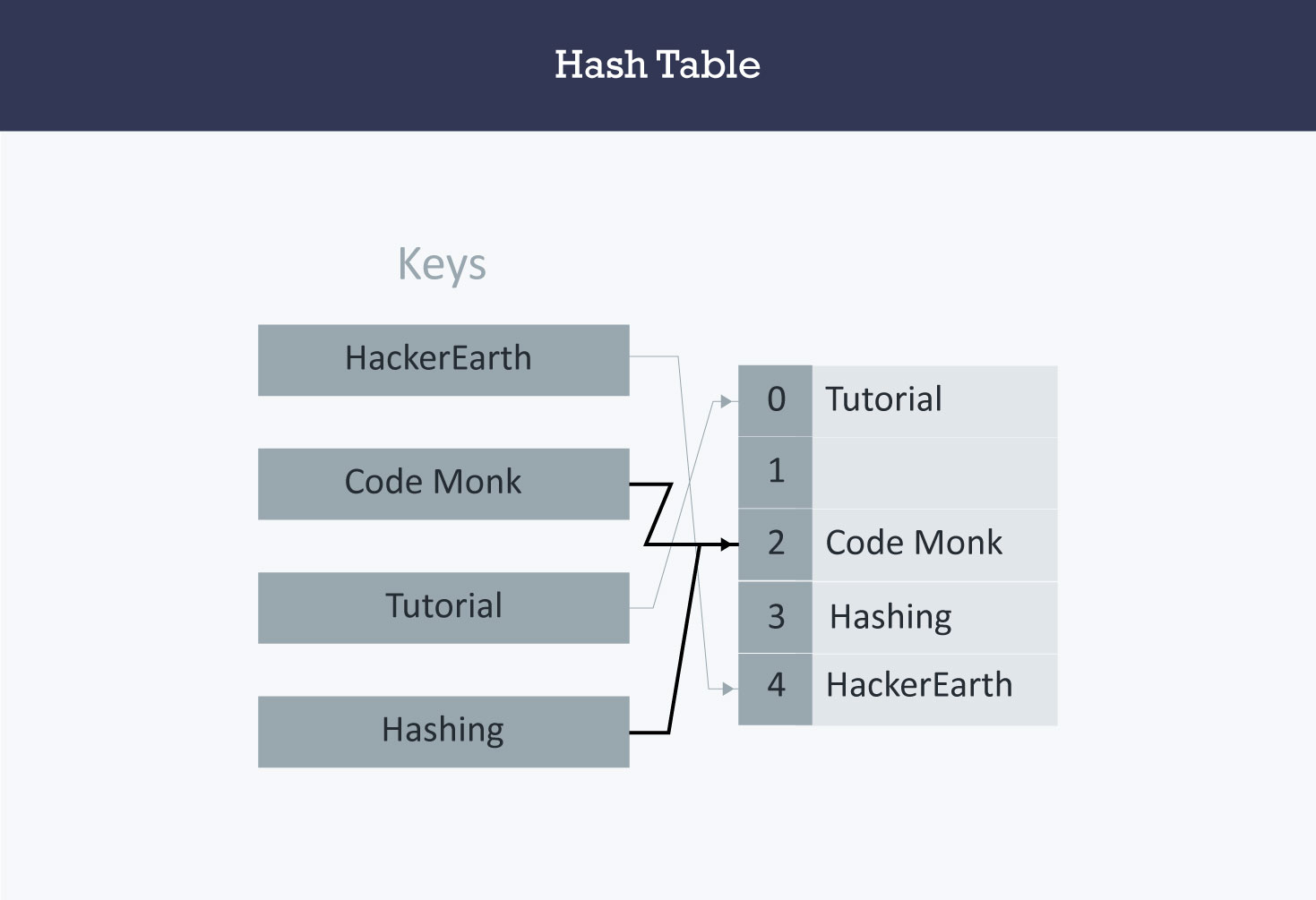
Binary Tree
Tree merupakan salah satu bentuk struktur data tidak linear yang menggambarkan hubungan yang bersifat hirarkis (hubungan one to many) antara elemen-elemen. Tree bisa didefinisikan sebagai kumpulan simpul/node dengan satu elemen khusus yang disebut Root dan node lainnya terbagi menjadi himpunan-himpunan yang saling tak berhubungan satu sama lainnya (disebut subtree). Untuk jelasnya, di bawah akan diuraikan istilah-istilah umum dalam tree :
A) Predecessor : node yang berada diatas node tertentu.
B) Successor : node yang berada di bawah node tertentu.
C) Ancestor : seluruh node yang terletak sebelum node tertentu dan terletak pada jalur yang sama.
D) Descendant : seluruh node yang terletak sesudah node tertentu dan terletak pada jalur yang sama.
E) Parent : predecessor satu level di atas suatu node.
F) Child : successor satu level di bawah suatu node.
G) Sibling : node-node yang memiliki parent yang sama dengan suatu node.
H) Subtree : bagian dari tree yang berupa suatu node beserat descendatnya dan memiliki semua karakteristik dari tree tersebut.
I) Size : banyaknya node dalam suatu tree.
J) Height : banyaknya tingkatan/level dalam suatu area.
K) Root : satu-satunya node khusus dalam tree yang tidak mempunyai predecessor.
L) Leaf : node-node dalam tree yang tidak memiliki successor.
M) Degree : banyaknya child yang dimiliki oleh suatu node.
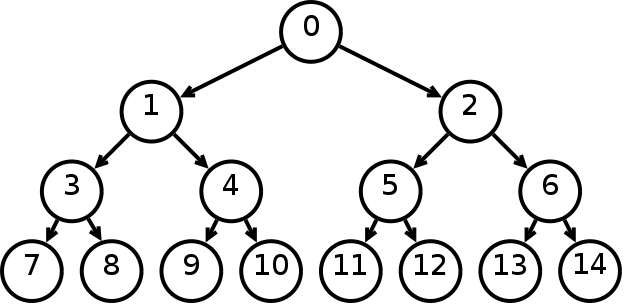
Maksimum node yang dapat dimiliki oleh sebuah level k dalam binary tree adalah 2k.
Binary Search Tree
Binary Search Tree mempunyai 2 aturan yaitu:
1. Jika value node lebih besar dari node, maka node tersebut akan menjadi leaf kanan node tersebut.
2. Jika value node lebih kecil dari node, maka node tersebut akan menjadi leaf kiri node tersebut.
Ini adalah contoh kode create dan insert untuk binary search tree:
#include<stdio.h>
#include<stdlib.h>
struct node{
int key;
struct node *left, *right;
};
// Function untuk membuat node baru
struct node *newNode(int item){
struct node *temp = (struct node *)malloc(sizeof(struct node));
temp->key = item;
temp->left = temp->right = NULL;
return temp;
}
void inorder(struct node *root)
{
if (root != NULL)
{
inorder(root->left);
printf("%d \n", root->key);
inorder(root->right);
}
}
/* Function untuk insert */
struct node* insert(struct node* node, int key){
if (node == NULL) {
return newNode(key);
}
if (key < node->key){
node->left = insert(node->left, key);
}else if (key > node->key){
node->right = insert(node->right, key);
}
return node;
}
int main(){
/* Kita akan membuat binary search tree seperti ini
50
/ \
/ \
30 70
/ \ / \
20 40 60 80 */
struct node *root = NULL;
root = insert(root, 50);
insert(root, 30);
insert(root, 20);
insert(root, 40);
insert(root, 70);
insert(root, 60);
insert(root, 80);
inorder(root);
return 0;
}
Contoh kode delete untuk binary search tree;
// C program to demonstrate delete operation in binary search tree
#include<stdio.h>
#include<stdlib.h>
struct node
{
int key;
struct node *left, *right;
};
struct node *newNode(int item)
{
struct node *temp = (struct node *)malloc(sizeof(struct node));
temp->key = item;
temp->left = temp->right = NULL;
return temp;
}
void inorder(struct node *root)
{
if (root != NULL)
{
inorder(root->left);
printf("%d ", root->key);
inorder(root->right);
}
}
/* Function untuk insert*/
struct node* insert(struct node* node, int key)
{
/* If the tree is empty, return a new node */
if (node == NULL) return newNode(key);
/* Otherwise, recur down the tree */
if (key < node->key)
node->left = insert(node->left, key);
else
node->right = insert(node->right, key);
/* return the (unchanged) node pointer */
return node;
}
struct node * minValueNode(struct node* node)
{
struct node* current = node;
/* loop down to find the leftmost leaf */
while (current && current->left != NULL)
current = current->left;
return current;
}
/* Function untuk delete */
struct node* deleteNode(struct node* root, int key)
{
// base case
if (root == NULL) {
return root;
}
if (key < root->key) {
root->left = deleteNode(root->left, key);
}else if (key > root->key) {
root->right = deleteNode(root->right, key);
} else{
if (root->left == NULL)
{
struct node *temp = root->right;
free(root);
return temp;
}
else if (root->right == NULL)
{
struct node *temp = root->left;
free(root);
return temp;
}
struct node* temp = minValueNode(root->right);
root->key = temp->key;
root->right = deleteNode(root->right, temp->key);
}
return root;
}
int main()
{
/* Kita akan membuat binary search tree seperti ini
50
/ \
30 70
/ \ / \
20 40 60 80 */
struct node *root = NULL;
root = insert(root, 50);
root = insert(root, 30);
root = insert(root, 20);
root = insert(root, 40);
root = insert(root, 70);
root = insert(root, 60);
root = insert(root, 80);
printf("Inorder traversal of the given tree \n");
inorder(root);
printf("\nDelete 20\n");
root = deleteNode(root, 20);
printf("Inorder traversal of the modified tree \n");
inorder(root);
printf("\nDelete 30\n");
root = deleteNode(root, 30);
printf("Inorder traversal of the modified tree \n");
inorder(root);
printf("\nDelete 50\n");
root = deleteNode(root, 50);
printf("Inorder traversal of the modified tree \n");
inorder(root);
return 0;
}
AVL Tree
AVL Tree adalah binary search tree yang telah disortir menjadi seimbang. AVL Tree merupakan nama dari kedua penemu AVL Tree yaitu G.M.Adelson Veleskii dan E.M.Landis.
Contoh AVL Tree:

Contoh Binary Search Tree yang belum di sortir:

Cara menentukan Height dan Balance Factor :
Height :
- Jika node (root) tidak memiliki subtree heightnya = 0
- Jika node adalah leaf, height = 1
- Jika internal node, maka height = height tertinggi dari anak + 1
Balance Factor :
-selisih height antara anak kiri dan kanan, jika tidak memiliki anak, dianggap 0.
Ada 2 jenis rotation dalam AVL Tree:
1. Single Rotation

2. Double Rotation
Rotasi pertama:

Rotasi kedua:

B-Tree
Pada B-Tree dikenal istilah order. Order menentukan jumlah maksimum/minimum anak yang dimiliki oleh setiap node, sehingga order merupakan hal yang cukup penting dalam B-Tree. 2-3 Tree pada postingan sebelumnya yaitu Balanced Binary Search Tree (AVL and RBT) and 2-3 Tree merupakan salah satu B-Tree berorder 3. Itu sebabnya setiap nodenya memiliki batasan anak, dengan minimal 2 anak dan maksimal 3 anak.
Aturan pada B-Tree:
- Setiap node (kecuali leaf) memiliki anak paling banyak sejumlah m anak
- Setiap node (kecuali root) memiliki anak paling sedikit m/2 anak
- Root memiliki anak minimal 2, selama root bukan leaf
- Jika node non leaf memiliki k anak, maka jumlah data yang tersimpan dalam node k-1
- Data yang tersimpan pada node harus terurut secara inorder
- Semua leaf berada pada level yang sama, level terbawah
Contoh 2-3 Tree:
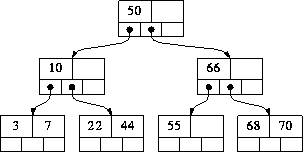
Contoh Order 4-5:

Heap and Tries
Heap
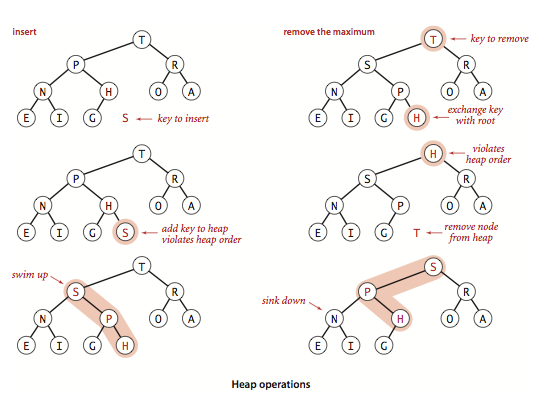
Heap adalah struktur data khusus berbasis pohon di mana pohon adalah complete binary tree. Umumnya, Heaps dapat dua jenis:
Max-Heap: dalam Max-Heap, key yang ada di node root harus terbesar di antara key yang ada di semua child. Properti yang sama harus dapat direkursif untuk semua sub-tree di binary tree.
Min-Heap: dalam Min-Heap, key yang ada di node root harus minimum di antara key yang ada di semua child. Properti yang sama harus dapat direkursif untuk semua sub-tree di binary tree.
· Min Heap
· Setiap node lebih kecil dari masing-masing childnya
· Root merupakan node paling kecil, sedangkan node terbesar terletak pada leaf node
· Max Heap
· Setiap node lebih besar dari masing-masing childnya
· Root merupakan node paling besar, sedangkan node terkecil terletak pada leaf node
· Min-Max Heap
· Heap dengan Min heap pada level ganjil dan Max heap pada level genap
Heap dapat diimplementasi dengan array maupun dengan linked list. Aplikasi heap adalah sebagai berikut:
· Priority Queue
· Selection algorithm
· Dijkstra's Algorithm
· Prim Algorithm
Implementasi heap menggunakan array;
· Array dimulai dengan indeks ke 1
· Rumus umum aplikasi heap dengan array (x adalah current node):
· Parent(x): x/2
· Left-child(x): 2*x
· Right-Child(x): 2*x+1
Min Heap
· Find-Min
· Minimum node terletak pada root
· Insertion pada Min-heap
· Insert node selalu berurutan dari level paling rendah dengan urutan left ke right
· New node selalu menjadi leaf node
· Sesuikan sesuai heap properties secara rekursif
· Deletion-Min pada Min-Heap
· Node yang dihapus selalu root karena merupakan node paling kecil, lalu diganti dengan node yang paling terakhir di insert
· Sesuaikan dengan heap properties secara rekursif
Max Heap
Insertion dan deletion untuk Max heap, hanya saja disesuakan dengan properties Max-Heap
Min-Max Heap
· Insert node sesuai urutan, lalu cek upheap lalu sesuaikan dengan properties level.
· Umumnya dilakukan penyesuaian rekursif dengan urutan sebagai berikut:
1. Parent
2. Grand Parent
· Deletion selalu dilakukan pada root, lalu sesuaikan dengan downheap sesuai properties
· Umumnya dilakukan penyesuaian secara rekursif dengan urutan sebahai berikut:
1. Grand child
2. Child ( grand child disesuaikan dengan parentnya)
Tries
· Tries adalah tree yang dilakukan untuk menyimpan array asosiatif
· Properties pada tries:
· Setiap vertex/node merepresentasikan satu huruf
· Root merepresentasikan karakter kosong
· Aplikasi pada trees adalah fitur auto-complete yang ada pada web-browser

Sumber :
https://www.geeksforgeeks.org/binary-search-tree-set-1-search-and-insertion


Comments
Post a Comment